DATA COMPRESSION

AND DECOMPRESSION

Definition:

In general data compression consists of taking a stream of symbols and transforming them into codes. If the compression is effective the resulting stream of codes will be smaller than the original symbols.

(A) LOSSY DATA COMPRESSION :

This is generally used for graphics image and digitized voice compression as it concedes a certain loss of accuracy in exchange for greatly increased compression.

(B) LOSSLESS DATA COMPRESSION :

This type of compression is used when storing database records, spreadsheets, or word processing files as it consists of those techniques guaranteed to generate an exact duplicate of the input data stream after compression.

DATA COMPRESSION = MODELING + CODING

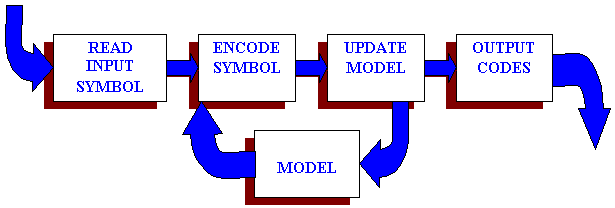
The model is simply a collection of data and rules used to process input symbols and determine which code(s) to output. A program uses a model to accurately define the probabilities for each symbol and the coders to produce an appropriate code based on those probabilities.

CODING:

Huffman and Shanon-Fano are two different ways of generating variable-length codes when given a probability table for a given set of symbols. These were the two coding methods that worked well. But the problem with these two methods is that they use an integral number of bits in each code. If the entropy of given character is 2.5 bits the Huffman code for that character must be either 2 or 3 bits, not 2.5. Because of this Huffman coding can’t be considered an optimal coding method but it is the best approximation that uses fixed codes with an integral number of bits.

SYMBOL	HUFFMAN CODE
E	100
T	101
A	1100
I	11010
---------
X	01101111
Q	01101110001
Z	01101110000

MODELING:

Loss-less data compression is generally implemented using one of two different types of modeling:

(I) STATISTICAL MODELING:

This method simply depended on knowing the probability of each symbol's appearance in a message. Given the probabilities, a table of codes could be constructed that served several important properties.

Different codes have different number of bits. Codes for symbols with low probabilities have more bits and codes for symbols with higher probabilities have fewer bits. Though the codes are of different bit lengths they can be uniquely decoded.

We have used the Huffman algorithm for statistical modeling.

SYMBOLS

CODES

GENERAL ADAPTIVE COMPRESSION

CODES

SYMBOLS

GENERAL ADAPTIVE DECOMPRESSION

(i) DICTIONARY BASED MODELING :

This method reads in input data and looks for groups of symbols that appear in a dictionary. If a string match is found, a pointer or index in the dictionary can be output instead of the code for the symbol. The longer is the match, the better the compression ratio.

Lossy compression accepts slight loss of data to facilitate compression. Lossy compression is generally done on analog data stored digitally, with the primary applications being graphics and sound files.

SIMULATION OF DATA COMPRESSION

AND DECOMPRESSION

DISCRETE SYSTEM:

Systems in which changes are predominantly discontinuous will be called as discrete systems. Here we use the concept of Discrete System Simulation.

SYSTEM DESCRIPTION:

The system of data compression could be defined as follows:

(i) The system takes a number of uncompressed files form a directory randomly and performs its compression using 3 algorithms namely Huffman compression algorithm, Arithmetic compression algorithm and the LZSS compression algorithm.

(ii) From the queue formed by the randomly selected uncompressed files, we select the files one by one and start the procedure of compression.

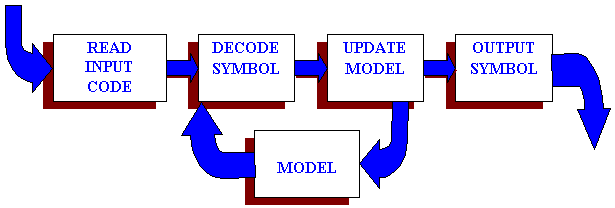
The system of data decompression could be defined as follows:

(i) The system takes a number of compressed files from a directory randomly and performs decompression using 3 algorithms namely Huffman decompression algorithm, Arithmetic decompression algorithm and the LZSS decompression algorithm. It decompresses files compressed by Huffman compression algorithm using Huffman decompression algorithm and so on.

(ii) From the queue formed by the randomly selected compressed files, we select the files one by one and start the procedure of decompression.

OBJECT OF SIMULATION:

The object of simulation will be to study how a particular algorithm is suited for compression and decompression of a particular type of file and at the end arrive at the conclusion as to which algorithm should be used to compress a particular type of file.

SIMULATION PROGRAMMING TASKS

(A) GENERATE MODEL:

Here we are fortunate enough to be able to work with the whole system itself rather than having to prepare a whole model for it.

SYSTEM IMAGE:

ENTITIES	ATTIRBUTES	ACTIVITIES
Compressed Files	File size, File type, Number of files	---
Decompressed Files	File size, File type, Number of files	---
Algorithms	Algorithm coding, Suitability, Principle	To compress and Decompress files

ROUTINES:

Take a file and compress it using all the algorithms. Take a compressed file and decompress it using the same algorithm.

(B) SIMULATATION ALGORITHM

Selection: We select random number of files from a directory randomly to form a queue. The queuing discipline is FIFO (First In First Out).

Find: Find the next file in the queue of files so generated to be compressed/decompressed.

Test: Test whether the selected file can be if uncompressed can be compressed or not. If the file is compressed it should be checked whether it could be decompressed or not.

If it cannot be compressed/decompressed then we select the next file from the queue. If the file can be compressed then we compress it using all the algorithms.

Change: Now we change the system image after compression/decompression of a file.

Gather statistics: Finally we gather the statistics of the compressing/decompressing system as shown above.

Count: Total number of files processed.

Number of files waiting in queue.

Summary measures: Mean value of compression ratio,

Variance,

Standard deviation.

VARIOUS ALGORITHMS USED FOR DATA COMPRESSION AND DECOMPRESSION:

HUFFMAN ALGORITHM:

Huffman coding creates variable length codes that are in integral number of bits. Symbols with higher probabilities get shorter codes. Huffman codes can be correctly decoded despite being of variable length. Decoding is done by following a binary decoder tree.

Huffman codes are built form the bottom up, i.e. from leaves progressively closer starting to the root.

BUILDING A TREE:

1. For a given list of symbols, develop a corresponding list of probabilities or frequency counts so that each symbol's relative frequency of occurrence is known.

2. Sort the lists of symbols according to frequency with the most frequently occurring symbols at the top and the least frequently occurring symbols at the bottom.

3. Divide the list into two parts, with the total frequency counts of the upper half being as close to the total of the bottom half as possible.

4. The upper half of the list is assigned the binary digit 0, and the lower half is assigned the digit 1. This means that the codes for the symbols in the first half will all start with 0, and the codes in the second half will all start with 1.

5. Recursively apply the steps 3 and 4 to each of the two halves, subdividing groups and adding bits to the codes until each symbol has become a corresponding code leaf on the tree.

For the values taken the Huffman code table can be given as:

A	B	C	D	E
15	7	6	6	5

The final Huffman tree can be given as:

ROOT

0 1

39 0 1

0 1 0 1

13 11 15 7 6 6 5

A B C D E

DETERMINING THE CODES:

To determine code for a given symbol, we have to walk from the leaf mode to the root of the tree, accumulating new bits as we pass through each parent node. But, as the bits are returned in the reverse order, we have to push the bits onto a stack, then pop them off to generate the code.

The codes here have a unique profile property. Since no code is a prefix to another code, Huffman codes can be unambiguously decoded as they arrive in a stream.

A	0
B	100
C	101
D	110
E	111

Since no code is a prefix to another code Huffman codes can be unambiguously decoded as they arrive in a stream. The symbol with the highest priority ‘A’ has been assigned the fewest bits and the symbol with lowest priority ‘E’ has been assigned the most bits.

INTO THE HUFFMAN CODE:

The Huffman coding process could be divided into 4 basic parts:

(I) Counting the Symbols:

To build the tree first the frequencies of symbols are calculated. This count is stored is in an array.

(II) Saving the Counts:

For expansion program to correctly expand the Huffman coded bit stream it will be receiving, it needs a copy of the Huffman tree identical to the one used by the encoder. This means that the tree or its equivalent must be passed as the header to the file so the expander can read it before it can start to read Huffman code. The easiest way for the expansion program to get this data would probably be to store the entire node array as a preamble to the compressed data.

(III) Building the Tree:

Whether compressing or expanding, once the counts have been loaded it is time to build Huffman tree. The actual process of creating the tree is the simple matter of sitting in a loop and combining the two free nodes with lowest weights into a new internal node with the combined weights of the nodes. Only one free node is left, the tree is done and the free node is the root of the tree.

(IV) Using the Tree:

During the expansion phase, it is easy to see how to use the Huffman tree. Starting at the root node, a single bit at a time is read by the decoder. If the bit is 0, the next node is the one pointed to by the child_0 index. If the bit is 1, the next node is the one pointed to by the child_1 index. If the new node is 256 or less we have reached a leaf of tree and can output the corresponding symbol. If the symbol was the special end-of-string symbol we can exit instead of sending it out.

ARITHMETIC CODING: (Improvement in Huffman algorithm)

Difficulties in Huffman coding:

Huffman codes have to be an integral number of long bits and this can sometimes be a problem. If the probability of a symbol is 1/3,for example, the optimum number of bits to code that symbol is around 1.6 bits. Huffman coding has to assign either one or two bits to the code, and either choice leads to a longer compressed message than is theoretically possible. This non-optimal coding becomes a noticeable problem when the probability of a symbol is very high. If a statistical method could assign a 90% probability to a given symbol the optimal code size would be 0.15 bits. The Huffman coding system would probably assign a one-bit code to the symbol, which is 6 times longer than necessary.

Arithmetic Coding:

Arithmetic coding replaces a stream of input symbols with a single floating point output number.

The encoding process is simply one of narrowing the range of possible numbers with every new symbol. The new range is proportional to the predefined probability attached to that symbol. Decoding is the inverse procedure, in which the range is expanded in proportion to the probability of each symbol as it is extracted.

The model for a program using arithmetic coding needs to have 3 pieces of information for each symbol:

(i) The low end of its range,

(ii) The high end of its range &

(iii) The scale of the entire alphabet

Since the top of a given symbol’s range is the bottom of the next, we only need to keep track of N+1 numbers for N symbols in the alphabet.

The encoding process consists of looping though entire file, reading in a symbol, determining its range variables, then encoding it. After the file has been scanned the final step is to encode the end-of-stream symbol.

After encoding, it is necessary to flush the arithmetic encoder. The code for this outputs 2 bits and any additional underflow bits added along the way.

During arithmetic decoding, the high and low variables should track exactly the same values they had during the encoding process, and the code variable should reflect the bit stream as it is read in from the input file.

Arithmetic encoding seems more complicated than Huffman encoding, but the size of the program required to implement it is not significantly different. Runtime performance is significantly slower than Huffman encoding, due to the computational burden imposed on encoder and decoder. If squeezing the last bit of compression capability out of the coder is important, arithmetic coding would always do as good a job or better, than Huffman encoding.

LZSS Algorithm:

LZSS is a dictionary-based compressor. It uses previously seen text as a dictionary. It replaces variable length phrases in the input text with fixed size pointers into the dictionary to achieve compression. The amount of compression depends on how long the dictionary phrases are and how large the window into the previously seen text is, and the entropy of the source text with respect to the LZSS model.

The main data structure in LZSS is a text window, divided into 2 parts. The 1^st part consists of a large block of recently decoded text. The 2^nd, normally much smaller is a look-ahead buffer. The look-ahead buffer has characters read in from the input stream but not yet encoded.

The normal size of the text window is several thousand characters. The look-ahead buffer is generally much smaller. The algorithm tries to match the contents of the look-ahead buffer to a string in the dictionary.

LZSS stores text in contiguous windows, but it creates an additional data structure that improves on the organization of the phrases. As each phrase passes out of the look-ahead buffer and into the encoded portion of the text windows, LZSS adds the phrase to a tree structure

By sorting the phrases into a tree such as this, the time required to find the longest matching phrase in the tree would be proportional to the base 2 logarithm of the window size multiplied with phrase length.

The savings created by using the tree not only make the compression side of the algorithm much more efficient but it also encourages experimentation with longer window sizes.

LZSS allows pointers and characters to be freely intermixed. Once the data is well characterized, the compressor may efficiently match up pointers every time it loads new data in to the look-ahead buffer.

DATA STRUCTURES IN LZSS ALGORITHM:

For every phrase in the window, a corresponding structure element defines the position that phrase occupies in the tree. Each phrase has a parent and up to two children. Since this is a binary tree the two child nodes are defined as 'smaller' and 'larger' children. Every phrase that resides under the smaller child node must be smaller than the phrase defined by the current node and every phrase under the larger child node must be larger than the phrase defined by the current node.

LOSSY COMPRESSION:

Lossy compression techniques are used to achieve very high level of data compression of continuous tone graphical images, such as digitized images of photographs.

Just like audio data graphical images have an advantage over conventional computer data files: they can be slightly modified during the compression/expansion cycle without affecting the perceived quality on the part of the user. Minor changes in the exact shade of a pixel here and there can easily go completely unnoticed, if the modifications are done carefully. A lossy compression program that doesn’t change the basic nature of the image ought to be visible.

THE DISCRETE COSINE TRANSFORM (DCT):

The key to the compression process discussed in the lossy compression is a mathematical transformation known as THE DISCRETE COSINE TRANSFORM (DCT). The DCT is in a class of mathematical operations that include the well-known Fast Fourier Transform (FFT).

Results for 3 files using lossy compression are shown in tabular form as below:

FILE	QUALITY FACTOR	STARTING SIZE	COMPRESSED SIZE	RATIO %	RMS ERROR
Cheetah.gs	5	64000	10232	85%	10.9
Cheetah.gs	10	64000	7167	89%	13.6
Cheetah.gs	15	64000	6074	91%	15.2
Cheetah.gs	25	64000	5094	93%	17.4

Clown.gs	5	64000	8636	87%	8.6
Clown.gs	10	64000	6355	91%	10.9
Clown.gs	15	64000	5513	92%	12.3
Clown.gs	25	64000	4811	93%	14.1

Lisaw.gs	5	64000	5941	91%	3.7
Lisaw.gs	10	64000	4968	93%	4.7
Lisaw.gs	15	64000	4563	93%	5.8
Lisaw.gs	25	64000	4170	94%	6.6

LOSSY COMPRESSION:-

Upper Part:

Decompressed by Quality Factor->25

Lower Part:

Original Picture

Input Bytes : 64000

Output Bytes : 5094

Compression ratio: 93%

RMS Error : 17.4